前端笔记:Transfrom: Matrix() 参数配置笔记
最近在学一些前端知识,学到 Martrix 可以用一行来将 Transfrom 的所有属性表达出来,就打算在网上找找如何操作,发现大部分都是讲一些高等数学的计算,或者一两个属性的转换,翻了好久才找到讲4个属性同时应用在 Matrix 上的教程。鉴于花了差不多5个小时才勉强弄懂 Matrix 的属性,我决定做一篇 Matrix 参数配置笔记。
目标:同时将 Translate, Rotate, Skew, Scale 属性应用在 Matrix 上。
首先在 2D 动画里面 Matrix 有6个参数,先用字母代替:
transform: matrix(A, B, C, D, E, F);
然后这6个字母要排列成一个矩阵,在后面属性叠加上要相乘。
矩阵里第一行代表 X 轴的变化,第二行代表 Y 轴的变化,第三行代表 Z 轴的变化,因为是 2D 动画不涉及 Z 轴,所以是默认的 0 0 1。
1.将位移属性 Translate 应用在 Matrix 上。
Translate(X, Y) 中的 X 值和 Y 值与矩阵里的 E 和 F 相等。
假如我有属性 Translate(10px, 20px),那么应该这样转换:
得到 transform: matrix(1, 0, 0, 1, 10, 20);
- 注意 A 和 D不能为0,没有数值时要填1。
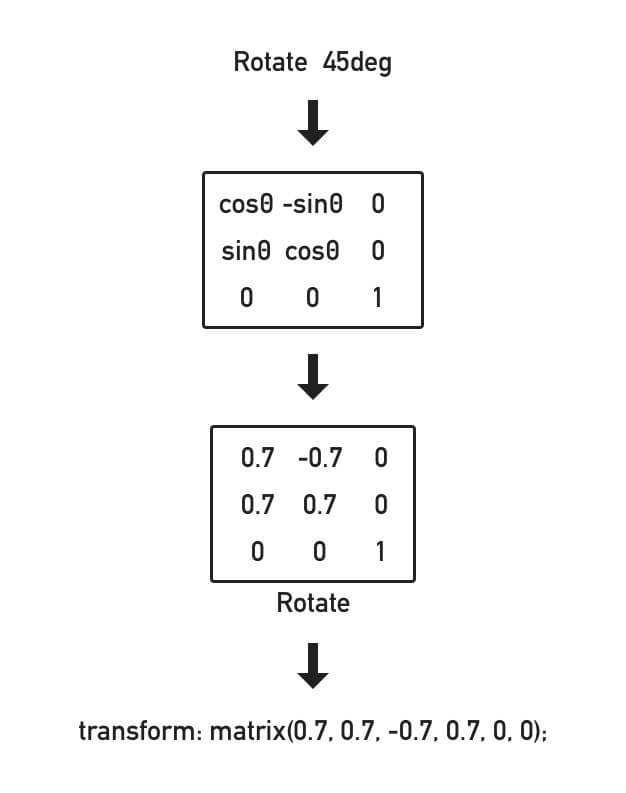
2.将旋转属性 Rotate 应用在 Matrix 上。
Rotate(θ) 的角度与矩阵中 A, B, C, D 是 cosθ, sinθ, -sinθ, cosθ 的关系,计算后代入即可。
假如我有属性 Rotate(45deg),那么应该这样转换:
得到 transform: matrix(0.7, 0.7, -0.7, 0.7, 0, 0);
3.将斜切属性 Skew 应用在 Matrix 上。
Skew 中的 α 和 β 值与矩阵中 B和 C 是 tanβ, tanα 的关系,计算后代入即可。
假如我有属性 Skew (30deg, 0deg),那么应该这样转换:
得到 transform: matrix(1, 0, 0.57, 1, 0, 0);
- 之前提到矩阵里第一行是 X 轴变换,第二行是 Y 轴变换,所以要注意 SkewX(α)对应的是矩阵第一行里的 C,而 SkewY(β) 对应的是矩阵第二行的 B。
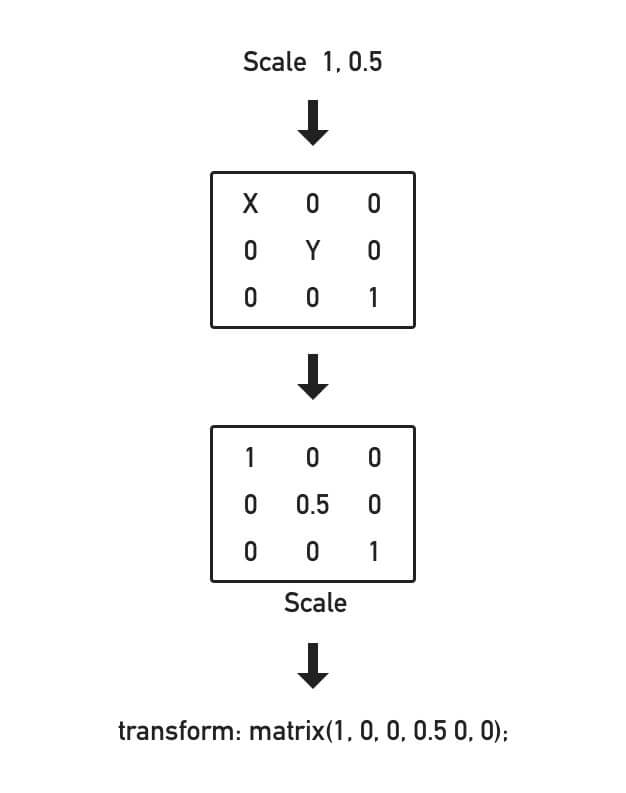
4.将缩放属性 Scale 应用在 Matrix 上。
Scale(X, Y) 中的 X 值和 Y 值与矩阵里的 A 和 D 相等。
假如我有属性 Scale (1, 0.5),那么应该这样转换:
得到 transform: matrix(1, 0, 0, 0.5 0, 0);
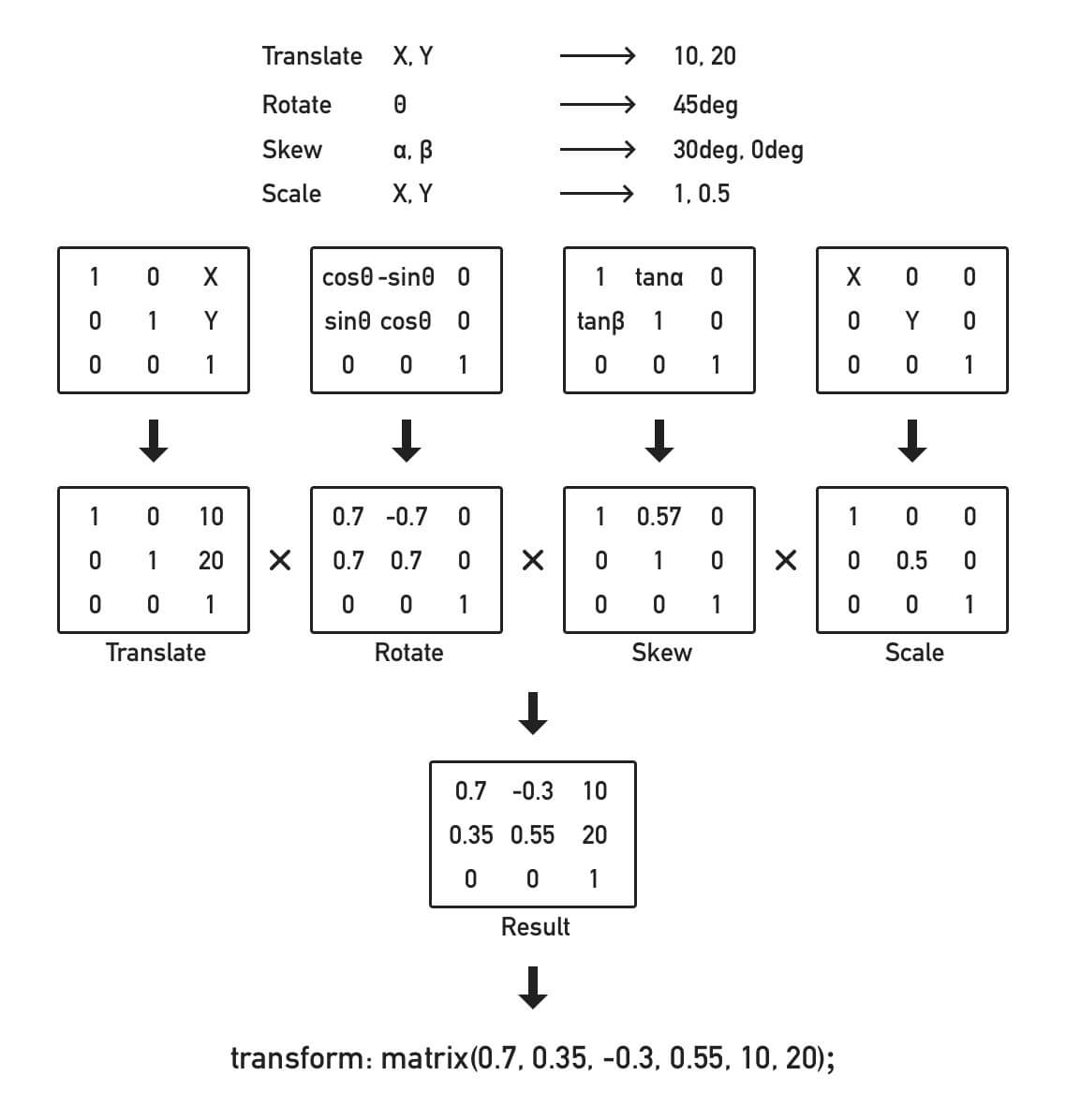
5.同时将4个属性转换应用在 Matrix 上。
使用矩阵计算器,按 Translate, Rotate, Skew, Scale 的顺序将这四个矩阵相乘,得到的矩阵写进 Transform: matrix() 里即可。
得到 transform: matrix(0.7, 0.35, -0.3, 0.55, 10, 20);